[ADSP] 3과목 - 5장 1-2. 데이터마이닝,성과분석,ROC/ 분류분석, 지니계수

Certificate/ADSP

[ADSP] 3과목 - 5장 1-2. 데이터마이닝,성과분석,ROC/ 분류분석, 지니계수

Istj_eff 2022. 10. 11. 23:55

1절. 데이터마이닝

1. 데이터 마이닝

: 대용량 데이터로부터 의미있는 관계, 규칙, 패턴을 찾는 과정

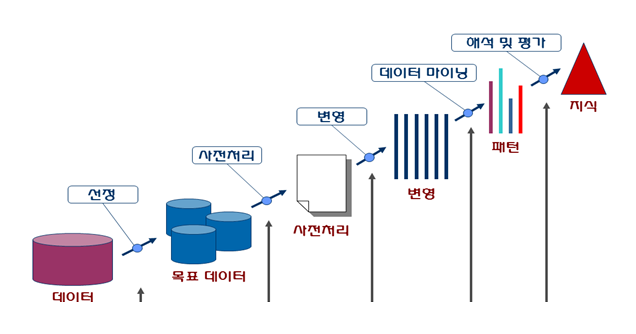
통계분석은 가설이나 가정에 따른 분석이나 검증을 하지만 데이터 마이닝은 다양한 수리 알고리즘을 이용해 데이터 베이스의 데이터로부터 의미있는 정보를 찾아내는 방법을 통칭한다.

1-2. 데이터마이닝의 종류

정보를 찾는 방법론에 따른 종류	인공지능(Artificial Intelligence) 의사결정나무(Decision Tree) K-평균군집합(K-means Clustering) 연관분석(Association Rule) 회귀분석(Regression) 로짓분석(Logit Analysis) 최근접이웃(Nearest Neighborhood)
분석대상, 활용목적, 표현방법에 따른 분류	시각화분석(Visualization Analysis) 분류(Classification) 군집화(Clustering) 포케스팅(Forecasting)

1-2. 사용분야

병원에서 환자 데이터를 이용해서 해당 환자에게 발생 가능성이 높은 병을 예측
기존 환자가 응급실에 왔을 때 어떤 조치를 먼저 해야 하는지를 결정
고객 데이터를 이용해 해당 고객의 우량/불량을 예측해 대출적격 여부 판단
세관 검사에서 입국자의 이력과 데이터를 이용해 관세물품 반입 여부를 예측

1-2. 데이터마이닝의 최근 환경

데이터마이닝 도구가 다양하고 체계화되어 환경에 적합한 제품을 선택하여 활용 가능하다.
알고리즘에 대한 깊은 이해가 없어도 분석에 큰 어려움이 없다.
분석 결과의 품질은 분석가의 경험과 역량에 따라 차이가 나기 때문에 분석 과제의 복잡성이나 중요도가 높으면 풍부한 경험을 가진 전문가에게 의뢰할 필요가 있다.
2000년대에 비즈니스 관점에서 데이터마이닝이 CRM의 중요한 요소로 부각되었다.

1-3. 데이터 마이닝의 추진단계

목적설정
데이터 준비 ★
- 데이터 정제를 통해 데이터 품질을 보장하고, 필요시 데이터를 보강하여 충분한 양의 데이터를 확보
가공 ★
- 모델링 목적에 따라 목적 변수 정의
- 필요한 데이터를 데이터 마이닝 소프트웨어에 적용할 수 있는 형식으로 가공
기법 적용
검증

2. 분석 목적에 따른 작업 유형과 기법

예측 (Predictive Modeling)	분류 규칙 (Classification)	- 가장 많이 사용되는 작업 - 과거 데이터로부터 고객특성을 찾아내어 분류모형을 만듬 - 이를 토대로 새로운 레코드의 결과값을 예측 - 목표 마케팅 및 고객 신용평가 모형에 활용됨	회귀분석 판별분석 신경망 의사결정나무
설명 (Descriptive Modeling)	연관 규칙(Association)	- 데이터 항목간의 종속관계를 찾아내는 작업 - 교차판매(Cross Selling), 매장진열(Display), 첨부우편(Attached Mailings), 사기적발(Fraud Detection) 등의 다양한 분야에 활용됨	동시 발생 매트릭스
	연속 규칙(Sequence)	- 연관 규칙에 시간관련 정보가 포함된 형태 - 고객의 구매이력(History) 속성이 반드시 필요 - 목표 마케팅(Target Marketing) 이나 일대일 마케팅(One to One Marketing)에 활용됨	동시 발생 매트릭스
	데이터 군집화(Clustering)	- 고객 레코드들을 유사한 특성을 지난 몇 개의 소 그룹으로 분할하는 작업 - 작업의 특성이 분류규칙(Classification)과 유사하나 분석대상 데이터에 결과값이 없음 - 판촉활동이나 이벤트 대상을 선정하는데 활용됨	군집분석

3.성과분석 오분류에 대한 추정치 ★★★★★

정분류율(Accuracy)	- 전체 관측치 중 실제값과 예측치가 일치한 정도 - 실제가 P일때 예측도 P, 실제가 N일때 예측도 N인 지점 (제대로 맞춘지점)/전부다 - TP + TN / TP + FN + FP + TN
오분류율(Error rate)	- 모형이 제대로 예측하지 못한 관측치 (= 1-정분류율)
재현율(Recall) =민감도(Sensitivity)	- 실제 True인 관측치 중 예측치가 적중한 정도 - 모형의 완전성을 평가하는 지표 - 실제가 P이고 예측도 P인 지점 / 실제가 P인 지점들 - TP / TP + FN
특이도(Specificity)	- False로 예측한 관측치 중 실제 값이 False인 정도 - 실제가 N이고 예측도 N인 지점 / 실제가 N인 지점들 - TN / FP + TN
정밀도 (Precison)	- True로 예측한 관측치 중 실제 값이 True인 정도 - 실제가 P일때 예측도 P인 지점 / 예측을 P로 한 지점들 - 식 : TP / (TP + FP)
F1지표	- 재현율과 정확도의 가중조화평균값

3-1. F점수 ★★

정확도에 주어지는 가중치를 베타(beta)라고 한다.
베타가 1인 경우를 특별히 F1점수라고 하고 값이 높을수록 좋음 ★
데이터가 불균형 할 때 사용
베타가 2인 경우, 재현율에 2배만큼의 가중치를 부여하여 조화평균을 하는 것이다. ★
2 * 정밀도(Precision) * 재현율(Recall) / 정밀도(Precision) + 재현율(Recall)

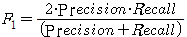
FP Rate 식 : FP / (FP + TN), 1 - Specificity(특이도)

FP Rate : 실제가 N인데 예측이 P로 된 비율 (Y가 아닌데 Y로 예측된 비율, 1종 오류)

4. ROC 그래프

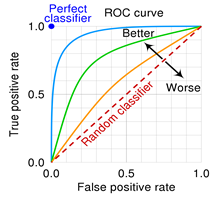
X축을 FPR(False Positive Rate=1-특이도)값으로 두고, Y을 TPR(Ture Positive Rate, 민감도)값으로 두어 시각화한 그래프이다.
2진 분류(Binary Classfication)에서 모형의 성능을 평가하기 위해 많이 사용되는 척도이다.
그래프가 왼쪽 상단에 가깝게 그려질수록 올바르게 예측한 비율은 높고, 잘못 예측한 비율은 낮음을 의미한다.
곡선 아래의 면적 AUROC(Area Under ROC) 값이 크면 클수록(1에 가까울수록) 모형의 성능이 좋다고 평가한다.
- TPR(Ture Positive Rate, 민감도) : 1인 케이스에 대한 1로 예측한 비율
- FPR(False Positive Rate, 1-특이도) : 0인 케이스에 대한 1로 잘못 예측한 비율
0.5에 가까울 수록 랜덤 모델에 가까운 좋지 못한 모형
Perfect classifier : 긍정,부정 모두 다 맞추는 위치 x=0, y=1인 경우!!!! ★★ classification성능이 우수하다고 봄,

5.이익도표

: 분류모형의 성능을 평가하기 위한 척도로, 분류된 관측치에 대해 얼마나 예측이 잘 이루어졌는지를 나타내기 위해
임의로 나눈 각 등급별로 반응검출율, 반응률, 리프트 등의 정보를 산출하여 나타내는 도표이다.

이익도표의 각 등급은 예측확률에 따라 매겨진 순위이기 때문에, 상위 등급에서는 더 높은 반응률을 보이는 것이 좋은 모형이라고 평가할 수 있다.
이익(gain) : 목표 번주에 속하는 개체들이 각 등급을 얼마나 분포하고 있는지 나타내는 값

이익도표(Lift)를 작성함에 있어 평가도구 중 %Captured Reponse를 표현한 계산식 :

해당 집단에서 목표변수의 특정범주 빈도 / 전체 목표변수의 특정범주 빈도 x 100 ★

# 무조건 암기

데이터 마이닝 단게 (특히 2,3)

오분류표 식

F1 계산 식

ROC

2절. 분류분석

1. 분류분석

데이터가 어떤 그룹에 속하는지 예측하는데 사용되는 기법이다.
클러스터링과 유사하지만, 분류분석은 각 그룹이 정의되어 있다.
교사학습(supervised learning)에 해당하는 예측기법이다.

1-1. 예측분석

시계열분석처럼 시간에 따른 값 두 개만을 이용해 앞으로의 매출 또는 온도 등을 예측하는 것
모델링을 하는 입력 데이터가 어떤 것인지에 따라 특성이 다르다.
여러 개의 다양한 설명변수(독립변수)가 아닌, 한 개의 설명변수로 생각하면 된다.

1-2. 분류분석, 예측분석의 공통점과 차이점

공통점
- 레코드의 특정 속성의 값을 미리 알아맞히는 점이다.
차이점
- 분류 : 레코드(튜플)의 범주형 속성의 값을 알아맞히는 것이다.
- 예측 : 레코드(튜플)의 연속형 속성의 값을 알아맞히는 것이다.

1-3.분류 모델링

신용평가모형 (우량, 불량)
사기방지모형 (사기, 정상)
이탈모형 (이탈, 유지)
고객세분화 (VVIP, VIP, GOLD, SILVER, BRONZE)

1-4. 분류 기법

회귀분석, 로지스틱 회귀분석 (Logistic Regression)
의사결정나무 (Decision Tree), CART(Classification and Regression Tree), C5.0
베이지안 분류 (Bayesian Classification), Naive Bayesian
인공신경망 (ANN, Artificial Neural Network)
지지도벡터기계 (SVN, Support Vector Machine)
K 최근접 이웃 (KNN, K-Nearest Neighborhood)
규칙기반의 분류와 사례기반추론(Case-Based Reasoning)

2. 로지스틱 회귀분석 (Logistic Regression)

독립변수(x)와 종속변수(y)사이의 관계를 설명하는 모형
독립변수가 연속형, 종속변수가 범주형★★(y=0 또는 1)값을 갖는 경우에 사용하는 방법
종속변수가 성공/실패, 사망/생존과 같이 이항변수로 되어 있을 때 종속변수와 독립변수간의 관계식을 이용하여 두 집단 또는 그 이상의 집단을 분류하고자 할 때 사용되는 분석기법

2-1. 로지스틱 회귀모형 특징

일반화선형모형의 특별한 경우로 로짓(logit) 모형으로도 불린다.
종속변수를 전체 실수 범위로 확장하여 분석하고, sigmoid 함수를 사용해 0~1값으로 변경
- probability(0~1) → odds → logit → sigmoid
logit : odds값에 log취함. 선형화의 하나, 값의 범위를 전체 실수 범위(-∞ ~ +∞)로 확장.
새로운 설명변수가 주어질 때, 반응변수의 각 범주에 속할 확률이 얼마인지 추정한다.
설명변수들의 관점에서 각 클래스의 관측치에 대한 유사성을 찾는데 사용 ★
설명변수가 한개일 때 회귀계수(β)의 부호에 따라 S자(β>0) 또는 역S자(β<0) 모양을 가짐
- (설명변수가 한개, 해당 회귀계수의 부호가 0보다 작은 경우 표현되는 그래프 : 역S자 ★)

# 승산비, 오즈비 (Odds ratio) ★

오즈는 성공할 확률이 실패할 확률의 몇배인지 나타내는 확률
승산(odds)비 = 성공률/실패율 = Pi/(1–Pi) (단, Pi는 성공률) ★
로지스틱의 회귀계수, 확률에 대해 0 ~ ∞ 로 변환한 값 ★
Optimizer는 최대우도법 사용, 모형검정은 카이제곱검정을 사용
성공 가능성이 높은 경우는 1보다 크고, 실패 가능성이 높은 경우는 1보다 작다
오즈(odds)의 관점에서 해석될 수 있다는 장점을 가진다.
exp(beta)의 의미는 나머지 변수가 주어질 때, 이 한 단위 증가할 때마다 성공(Y=1)의 오즈(odds)가 몇 배 증가하는지 나타내는 값 ★ (괄호뚫고 주관식문제)

2-2.선형회귀분석 vs 로지스틱 회귀분석

구분	일반 선형 회귀분석	로지스틱 회귀분석
종속변수	연속형 변수	이산형 변수
모형 탐색 방법	1) 최소자승법 ★	2) 최대우도법, 가중최소자승법
모형 검정	F 검정, t 검정	3) 카이제곱 검정 ★

1) 최소자승법(최소제곱법) ★★

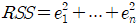
데이터와 추정된 함수가 얼마나 잘 맞는지는 잔차들을 제곱(square)해서 구한다. 이를 잔차제곱합(RSS or SSE)이라고 한다.
최소제곱법은 해당 식이 제곱형태이니 미분해서 0이 되는 지점을 찾기 위해 잔차제곱합을 최소화하는 계수를 구하는 방법이다.
- 최소제곱 ★ : 자료를 가장 잘 설명하는 회귀계수의 추정치는 보통 제곱오차를 최소로 하는 값을 구하며, 이 회귀계수 추정량을 최소제곱이라고 한다. (단답으로 나왔음)

2) 최대우도법

관측 값이 가정된 모집단에서 하나의 표본으로 추출된 가능성이 가장 크게 되도록 하는 회귀계수 추정방법
표본의 수가 클 경우에 최대우도법은 안정적이다.

3) 카이제곱 검정 ★

범주별로 관측빈도와 기대빈도의 차이를 통해서 확률모형이 데이터를 얼마나 잘 설명하는지검정하는 통계적 방법
독립변수와 종속변수가 모두 명목척도일 경우 적합한 통계 기법
정규모집단으로부터 N개의 단순임의추출한 표본의 분산은 카이제곱분포를 따른다.
- 일원 카이제곱검정: 적합성 검정 - 모집단이 특정한 분포를 따른다는 가설에 대해 검정
  - 한개의 범주집단이 대상
- 이원 카이제곱검정: 독립성 검정 - 표본 추출시 두 이산형 변량에 대한 독립성 여부 조사
동질성 검정 - 두집단 이상에 각 범주간의 비율이 서로 동일한지 검정
x^2분포는 t분포와 정규분포와는 달리 좌우대칭이 아니며 오른쪽으로 긴 꼬리를 갖는다.
제곱합의 합으로 구하기 때문에 음수는 가질 수 없고 다만 가장 왼쪽에서는 0의 값을 갖는다.

3. 의사결정나무(decision tree)

의사결정규칙을 나무 구조로 나타내 분류하거나 예측을 수행하는 분석방법
의사결정나무는 분류(classification)와 회귀(regression) 모두 가능하다.
분리기준 : Split criterion, 순수도가 높아지는 방향. 불확실성이 낮아지는 방향으로 분리
불순도 측도인 엔트로피 개념은 정보이론의 개념을 기반으로 하여, 임의의 사건이 모여있는 집합의 순수성(purity) 또는 단일성(homogeneity) 관점의 특성을 정량화해서 표현한 것 ★

대표적 적용 사례: 대출신용평가, 환자 증상 유추, 채무 불이행 가능성 예측 ★

장점	단점
분석과정이 직관적이고 이해하기 쉽고 해석이 용이하다.	분류 기준값의 경계선 부근의 자료값에 대해서는 오차가 크다. (비연속성)
선형성, 정규성, 등분산성 등의 수학적 가정이 불필요한 *비모수적 모형	로지스틱회귀와 같이 각 예측변수의 효과를 파악하기 어렵다.
수치형/범주형 변수를 모두 사용할 수 있다.	새로운 자료에 대한 예측이 불안정할 수 있다.
분류 정확도가 좋은 편이다. 대용량 데이터에서도 빠르다. 다중공선성 영향을 안 받는다. 비정상 잡음에 대해서도 민감하지 않음	설명변수간의 중요도를 판단하기 쉽지 않다.

비모수적 : 모수에 대한 가정을 전제로 하지 않고 모집단의 형태에 관계없이 주어진 데이터에서 직접 확률을 계산

3-1. 가지치기(Pruning) ★

최종 노드가 너무 많으면 과대적합(Overfitting) 가능성이 커져서 이를 해결하기 위해 사용
분류 오류를 크게 할 위험이 높으나 부적절한 규칙을 가지고 있는 가지를 제거하는 작업
가지치기 비용함수(Cost function)을 최소로 하는 분기를 찾아내도록 학습

3-2. 정지규칙(Stopping rule) ★

의사결정나무에서 더 이상 분기가 되지 않고 현재의 마디가 끝마디가 되도록 하는 규칙
‘불순도 감소량’이 아주 작을 때 정지함

3-3. 이산형 목표변수와 연속형 목표변수 ★

목표(=종속)변수가 범주형(이산형)인 경우 분류나무, 목표변수가 수치형(연속형)인 경우 회귀나무를 사용
이산형 목표변수 : p 값은 작을수록, 지니지수와 엔트로피지수는 클수록노드 내의 이질성이 크고 순수도가 낮다고 할 수 있다.
연속형 목표변수 : p값은 작아지고 분산의 감소량은 커질 수록 이질성이 높다.

	(1) 이산형 목표변수 (분류나무)	(2) 연속형 목표변수 (회귀나무)
(3) CHAID	카이제곱 통계량	ANOVA F 통계량
(4) CART ★	지니계수	분산 감소량
(5) C5.0 ★	엔트로피지수

표 암기!!

(1) 목표변수가 ‘이산형’ 목표변수인 경우 분류 기준

각 범주에 속하는 빈도에 기초하여 분리
오차율 분할 (잘못 분류된 관찰값의 수 / 전체 관찰값의 수)
카이제곱 통계량의 유의 확률(p-value) : 가장 작은 값을 갖는 방법 선택,
각 셀에 대한 (기대도수-실제도수)^2/기대도수 의 합
엔트로피지수 : 불순도 측정 지표, 가장 작은 값을 갖는 방법 선택

(2) 목표변수가 ‘연속형’ 목표변수인 경우 분류 기준 ★

평균과 표준편차에 기초하여 분리
잔차제곱합(SSR) 개선되는 방향으로 분할 (불필요한 지도학습 / 분산은 높고 편향은 낮다.)
F통계량 : 모델,모델 성분의 유의성을 검정하는 분산분석(ANOVA) 방식에 대한 검정통계량
분산감소량 : 예측오차를 최소화하는 것과 동일한 기준으로, 분산의 감소량을 최대화하는 기준의 최적분리에 의해 자식 마디가 형성.

(3) CHAID (Chi-squared Automatic Interaction Detection)

가지치기 하지않고 적당한 크기에 나무모형의 성장을 중지.
입력변수가 반드시 범주형

(4) CART (Classification And Regression Tree) ★

가장 많이 활용.
불순도의 측도로 목적변수가 범주형일 경우 지니지수를 이용, 연속형인 경우 분산을 이용한 이진분리(binary split)를 사용한다.
개별 입력변수뿐아니라 입력변수들의 선형결합들중 최적의 분리 찾음

(5) C5.0 ★

각 마디에서 다지분리(multiple) 가능.
범주형 입력변수에 대해 범주의 수만큼 분리됨
불순도의 측도로는 엔트로피지수를 이용

3-4. 지니 계수 ★ ★

불순도 측정 지표, 값이 작을수록 순수도가 높음 (분류잘됨)
불평등 지수를 나타낼 때 사용하는 계수로 0이 가장 평등, 1로 갈수록 불평등
범주가 두개일 때 한쪽 범주에 속한 비율(p)이 0.5일 때 불순도가 최대
지니지수 식 : 1- ∑(각 범주별수/전체수)²
- 예) ◈◈▣▣ 불순도 측정결과 지니지수는? 1-((2/4)² + (2/4)²) = ½

3-5. 학습의 불안정성

작은 병화에 의해 예측 모형이 크게 변하는 경우, 그 학습 방법은 불안정
가장 안정적인 방법 : K-최근접이웃, 선형회귀 모형
가장 불안정한 방법 : 의사결정 나무

저작자표시 비영리 변경금지 (새창열림)