4절. 시계열 분석
1. 시계열 자료
- 시간의 흐름에 따라 관찰된 값들을 시계열 자료라고 한다.
- 시계열 데이터 분석을 통해 미래를 예측하고 경향, 주기, 계절성 등을 파악하여 활용 ★
- 정상성 시계열 자료 : 비정상 시계열을 핸들링해 다루기 쉬운 시계열 자료로 변환한 자료
- 비정상성 시계열 자료 : 시계열 분석을 실시할때 다루기 어려운 자료
- 시계열 데이터의 구성요소 : 추세, 순환, 계절변동, 불규칙 변동 등 ★
- 분석 절차 ★
- 시간 그래프 그리기
- 추세와 계절성을 제거
- 잔차를 예측
- 잔차에 대한 모델 적합하기
- 예측된 잔차에 추세와 계절성을 더해 미래 예측

1-1. 시계열 구성 요소 ★★★
(1) 추세 요인 : 장기적으로 변해가는 큰 흐름 → 상승, 하락, 이차식, 지수식 형태
(2) 계절 요인 : 요일, 월, 분기 등 고정된 주기에 따른 변화
(3) 순환 요인 : 명백한 이유없이 알려지지 않은 주기를 가지고 변화
(4) 불규칙 요인
- 불규칙하게 변동하여 급격한 환경변화, 천재지변 같은 것으로 발생하는 변동
- 위 세 가지 요인으로 설명할 수 없는 회귀분석의 오차에 해당하는 요인
2. 정상성(Stationary)
- 확률과정의 평균과 분산이 일정하고, 주기적 변동이 없다는 것
- 미래는 확률적으로 과거와 동일하다는 것
2-1. 정상성의 조건 ★
(1) 평균은 모든 시점에 일정
(2) 분산은 모든 시점에 일정
(3) 공분산은 “시차”에만 의존★, 시점 자체에는 의존하지 않음
- 위 3가지 조건을 만족하지 못하는 경우 비정상시계열이며, 대부분의 자료가 비정상 시계열
- 시계열 자료의 분석을 위해서는 이를 판단하고, 분석 가능한 형태로 바꾸는 작업이 필요함

2-2. 정상시계열로 전환방법 ★
- 평균이 일정하지 않을 : 원계열에 차분 사용
- 계절성을 갖음 : 계절 차분 사용
- 분산이 일정하지 않을때: 원계열에 자연로그(변환) 사용 (ㅂ-ㅂ으로 암기)
- 차분 : 현 시점의 자료 값에서 전 시점의 자료 값을 빼는 것 ★★

3. 시계열 자료 분석방법
이동평균법
- 과거부터 현재까지 시계열 자료를 대상으로 일정기간별 이동평균을 계산하고, 이들의 추세를 파악하여 다음 기간을 예측하는 방법
- 시계열 자료에서 계절변동과 불규칙변동을 제거하여 추세변동과 순환변동만 가진 시계열로 변환하는 방법으로도 사용됨
- n개의 시계열 데이터를 m기간으로 이동평균하면 n-m+1개의 이동평균 데이터가 생성됨
지수평활법(Exponential Smoothing)
- 단기간에 발생하는 불규칙변동을 평활하는 방법
- 일정기간의 평균을 이용하는 이동평균법과 달리 모든 시계열자료를 사용하여 평균을 구하며, 시간의 흐름에 따라 최근 시계열에 더 많은 가중치를 부여하여 미래를 예측하는 방법
- 평활법: 변화가 심한 시계열 데이터를 평탄하고 변화가 완만하게 값을 변환시키는 것 ★
4. 시계열 모형
4-1. AR 모형자기회귀모형 ★
- 시계열 모델 중 자신의 과거 값을 사용하여 설명하는 모형 ☆
- AR(p) : 현시점의 자료가 p시점 전의 유한 개의 과거 자료로 설명될 수 있음.
- 백색잡음의 현재값과 자기 자신의 과거값의 선형 가중합으로 이루어진 정상 확률 모형 ☆
- 시계열자료의 시점에 따라 1차,2차,…,p차 등을 사용하나 정상시계열 모형에서는 주로 1,2차를 사용함. ☆
- 과거 시점의 관측 자료의 선형 결합으로 표현하는 것
4-2. MA 모형 이동평균모형 ★
- 최근 데이터의 평균을 예측치로 사용하는 방법, 각 과거치는 동일 가중치가 주어짐
- 현시점의 자료를 p시점 전까지 유한 개의 과거 백색잡음들의 선형결합으로 표현되어있어서 항상 정상성을 만족하는 모형으로, 정상성 가정이 필요없다.
- 백색 잡음의 현재값과 자기 자신의 과거값의 선형 가중합으로 이루어진 정상 확률 모형
- MA(p) : 과거 p시점 이전 오차들에서 현재항의 상태를 추론한다.
4-3. ARIMA 모형 자기회귀 누적이동평균모형 ★

- ARIMA는 AR모형과 MA모형을 합친 모형이다. AR(p) + MA(q)
- 자동회귀이동평균(ARMA : Autoregressive moving average) 모델의 일반화
- 기본적으로 비정상 시계열 모형
- 차분, 변환을 통해 AR모형이나 MA모형, ARMA 모형으로 정상화
- ARIMA(p,d,q)
- p : AR모형
- d : 차분 횟수 ★
- q : MA모형 차수
- ARIMA(1,2,3) 이라면 2번 차분해서 ARMA 모형이 될 수 있음
- ARIMA(p,d,q)
5. ACF, PACF, White Noise
- 자기상관함수 ACF : 시계열 데이터의 자기상관성을 파악하기 위한 함수
- 시계열의 관측치 Yt 와 Yt-k간 상관계수를 k의 함수 형태로 표시한 것, (k:시간단위)
- -1 ≤ autocorr(Yt, Yt-k) ≤ 1, k가 커질수록 ACF는 0으로 수렴함
- 부분자기상관함수 PACF : Yt 와 Yt-k 중간에 있는 값들의 영향을 제외시킨
- Yt 와 Yt-k사이의 직접적 상관관계를 파악하기 위한 함수
- 백색잡음 white noise
- 시계열 자료중 자기상관이 전혀 없는 특별한 경우
- 시계열의 평균이 0, 분산이 일정한 값, 자기공분산이 0인 경우
- 현재값이 미래 예측에 전혀 도움이 되지 못함
- 회귀분석의 오차항과 비슷한 개념

| 자기회귀 AR | 이동평균 MA | ARMA | |
| 자기상관함수 ACF | 지수적 감소 | q+1차항부터 절단모양 | q+1차항부터 절단모양 |
| 부분자기상관함수 PACF | p+1차항부터 절단모양 | 지수적 감소 | p+1차항부터 절단모양 |

분해 시계열 ★
- 상시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법
- 시계열에 영향을 주는 일반적인 요인을 분리해 분석 하는 방법
- 분해 요인 : 추세, 계절, 순환, 불규칙 요인 ★
5절. 다차원척도법(Multidimensional scaling, MDS)
다차원척도법 (MDS)
- 개체들의 유사성을 2차원,3차원 으로 표현하는 방법
- 여러 대상 간의 관계에 대한 수치적 지료를 이용해 유사성에 대한 측정치를 상대적 거리 로 시각화 하는 방법 ★★
- 군집분석과 같이 개체들을 대상으로 변수들을 측정한 후에 개체들 사이의 유사성/ 비유사성을 측정하여 개체들을 2차원 공간상 에 '점' 으로 표현하는 분석방법
즉 비슷한 개체들끼리 모아서 2차원 그래프로 표현해주는것
- 입력데이터 는 케이스 간의 유사도(similarity)를 측정한 거리 데이터이며, 출력 결과는 케이스들이 기하학적 공간상에 배치된 그래프
- 기하학적 공간상에 배치된 케이스 간의 거리는 유사도의 크기를 나타낸다.
즉 유사한 케이스 들은 서로 가까이 위치 하도록 배치, 상이한 케이스 들은 멀리 떨어져 있도록 배치해야 한다.
다차원척도법 방법
- 개체들의 거리 계산에는 유클리드 거리행렬을 활용한다.
- 관측대상들의 상대적 거리의 정확도를 높이기 위해 적합 정도를 스트레스값(strees value)으로 나타낸다.
다차원 척도법의 목적
- 데이터 속에 잠재되어 있는 패턴 또는 구조 를 찾아낸다.
- 그 구조를 소수 차원의 공간에 기하학적 으로 표현한다.
- 데이터 축소(Data Reduction)의 목적으로 다차원척도법을 이용한다.
즉, 데이터에 포함되는 정보를 끄집어내기 위해 다차원척도법을 탐색수단으로써 사용한다.
- 다차원척도법에 의해서 얻은 결과를, 데이터가 만들어진 현상이나 과정에 고유의 구조로서 의미를 부여한다.
- cmdscale(eurodist) : 각 도시의 상대적 위치 를 도식화할 수 있는 X, Y좌표 계산
- 특정 변수들의 관측치가 없더라도 개체 간의 유사성에 대한 자료 사용하여 산점도 그릴 수 있다.
다차원척도법 종류
1. 계량적 MDS (Metric MDS)
- 데이터가 구간척도나 비율척도인 경우 활용한다.

2. 비계량적 MDS (Monmetric MDS)
- 데이터가 순서척도인 경우 활용한다.
- 개체들간의 거리가 순서로 주어진 경우에는 순서척도를 거리의 속성과 같도록 변환하여 거리를 생성한 후 적용한다. ★
6절. 주성분 분석(PCA)
1. 주성분 분석(PCA, Principal Component Analysis) ★
- 공분산행렬, 상관계수행렬을 사용해 모든변수들을 가장 잘 설명하는 주성분을 찾는 방법
- 데이터에 많은 변수가 있을 때 변수의 수를 줄이는 차원 감소 기법
- 상관관계가 높은 변수들을 선형결합하여 새로운변수 만들고 분산을 최대화하는 변수로 축약
- 분산비율(Proportion of Variance) : 각 분산이 전체분산에서 차지하는 비중
- 누적비율(Cumulative proportion) : 주성분이 설명하는 전체분산양을 알수 있음(분산비율과 헷갈리지 말기!)
- 80%이상 자료를 설명하려면 최소 2개의 주성분이 필요
- 주성분들은 상관관계가 없다.
2. 주성분분석 개수(m)를 선택하는 방법 ★☆
- 전체 변이 공헌도 방법 : 전체 변이의 70~90% 전도가 되도록 주성분의 수를 결정한다.
- 평균고유값 방법: 고유값들의 평균을 구한 후 평균값 이상이 되는 주성분을 설정 (삭제아님!!)
- Scree graph: 고유값 산점도를 그린 그래프에서 감소 추세가 원만해지는 지점에서 1을 뺀 개수를 주성분의 개수로 선택한다.
- 주성분은 변수들의 계수구조를 파악하여 적절하게 해석되어야 하며, 명확하게 정의된 해석 방법이 있는 것은 아니다.

3. 공분산 행렬(default) vs 상관계수 행렬
- 공분산행렬은 측정단위를 그대로 반영, 상관계수 행렬은 모든 변수의 측정단위를 표준화함.
- 설문조사처럼 모든 변수들이 같은 수준으로 점수화된 경우 공분산행렬을 사용
- 변수들의 scale이 서로 많이 다른 경우엔 상관계수행렬을 사용
- 주성분 분석에서 상관계수 행렬 사용 : prcomp(data, scale=TRUE) = princomp(data, cor=TRUE)
- cov2cor() : 공분산행렬을 상관계수행렬로 변환하는 함수
- cor() : 상관계수행렬을 구하는 함수

- 17번째 줄에서 공분산행렬에서 상관계수행렬로 변환했고, 23번째 줄에서 상관계수 행렬을 구했다.
- 18~22번째 줄은 공분산행렬에서 상관계수로 변환한 결과이고, 24~28번째 나타난 상관계수행렬을 직접구한 결과가 동일하다.
4. 주성분분석 vs 요인분석
- 자료의 축소라는 차원에서 같은 의미로 해석하기 쉬우나 다른 개념
- 공통요인분석 : 자료의 축소라는 의미도 포함해 데이터에 내재적 속성까지 찾아내는 방법
| 주성분분석 | 요인분석 | |
| 공통점 | 모두 데이터를 축소하는데 활용된다. 원래 데이터를 활용해서 몇 개의 새로운 변수들을 만들 수 있다. | |
| 생성된 변수의 수 | 제 1주성분, 제 2주성분, 제 3주성분 정도로 활용된다. (대개 4개 이상은 넘지 않음) | 몇 개라고 지정 없이 만들 수 있다. |
| 생성된 변수의 이름 | 제 1주성분, 제 2주성분 등으로 표현된다. | 분석자가 요인의 이름을 명명한다. |
| 생성된 변수들 간의 관계 | 제1주성분이 가장 중요하고 그 다음 제2주성분이 중요하게 취급된다. |
새 변수들은 기본적으로 대등한 관계를 갖고 '어떤 것이 더 중요하다' 는 없다. 단, 분류/예측에 그 다음 단계로 사용된다면 그때 중요성의 의미가 부여된다. |
| 분석 방법의 의미 | 목표변수를 고려하여 잘 예측/분류하기 위하여 원래 변수들의 선형 결합으로 이루어진 몇 개의 주성분(변수)들을 찾아내게 된다. | 목표변수를 고려하지 않고 그냥 데이터가 주어지면 변수들을 비슷한 성격들로 묶어서 새로운 (잠재) 변수들 만든다. |
5. 주성분분석 예시
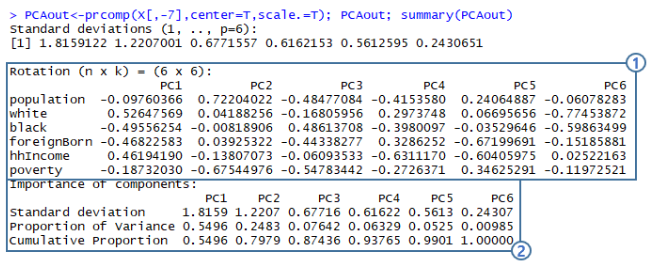
(1) Rotation : 실제로 원래의 독립변수에 곱해서 주성분을 만들 계수들을 나타낸다.
- 예를들어 PC1을 만들기 위해선 population에 −0.098, white에 0.056, ... , poverty에 −0.187 곱한 뒤 모두 더해서 만들어진다.
- 또한 데이터에 따라선 어떤 주성분이 어떤 변수에 대한 정보를 많이 가지고 있는지 한 눈에 확인할 수 있는 지표가 되기도 한다.
(2) Importance of components : 말그대로 각 주성분의 중요도를 나타낸다. Proportion of Variance가 높을수록 데이터의 많은 부분을 설명하고 그만큼 중요한 주성분이라는 의미가 된다.
'Certificate > ADSP' 카테고리의 다른 글
| [ADSP] 3과목 - 5장 3-4. 앙상블 분석, 인공신경망 분석 (0) | 2022.10.12 |
|---|---|
| [ADSP] 3과목 - 5장 1-2. 데이터마이닝,성과분석,ROC/ 분류분석, 지니계수 (0) | 2022.10.11 |
| [ADSP] 3과목 - 4장.통계분석, 기초통계분석, 회귀분석 (0) | 2022.10.09 |
| [ADSP] 3과목 1-3장. 데이터 분석, R, 데이터마트 (0) | 2022.10.09 |
| [ADSP] 2과목 - 데이터 분석 기획, 빅데이터, 분석 마스터 플랜 (0) | 2022.10.06 |




댓글